【算法】双指针

本文记录了近期在leetcode上刷到的关于双指针的题目。
由于数据特征的有序性(大小或者正负),所以可以证明当前节点一定是优于过往节点,从而可以通过数据的维度数量的指针,逐步的迭代收敛最终找到最优解。
无序数据大多只能通过遍历的方式来解决,因为无法通过指针的移动来证明当前节点是否是最优解。
回文字符串判断
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。
字母和数字都属于字母数字字符。
给你一个字符串 s,如果它是 回文串 ,返回 true ;否则,返回 false 。
示例 1:
输入: s = "A man, a plan, a canal: Panama"
输出:true
解释:"amanaplanacanalpanama" 是回文串。
示例 2:
输入:s = "race a car"
输出:false
解释:"raceacar" 不是回文串。
示例 3:
输入:s = " "
输出:true
解释:在移除非字母数字字符之后,s 是一个空字符串 "" 。
由于空字符串正着反着读都一样,所以是回文串。
提示:
1 <= s.length <= 2 * 105
s 仅由可打印的 ASCII 字符组成
kotlin速通
class Solution {
fun isPalindrome(s: String): Boolean {
val cleanedString = s.lowercase().replace(Regex("[^a-z0-9]"), "")
return cleanedString == cleanedString.reversed()
}
}
使用方便的扩展函数结合正则表达式替换,可以一两行输出结果。
思路1 使用封装好的库函数处理
去除多余字符,转换为小写,翻转,与原来的做比较:
class Solution {
public:
bool isPalindrome(string s) {
// 去除掉所有非字母数字的其他字符
s.erase(remove_if(s.begin(), s.end(),
[](unsigned char c) { return !isalnum(c); }),
s.end());
// 转换为小写
transform(s.begin(), s.end(), s.begin(), ::tolower);
// 反转字符串
string reversed = s;
reverse(reversed.begin(), reversed.end());
// 比较反转后的字符串是否与原字符串相同
return reversed == s;
}
};
优化调用库函数
将字符的剔除,转换合二为一:
class Solution {
public:
bool isPalindrome(string s) {
string sgood;
for (char ch: s) {
// 剔除非字母数字字符
if (isalnum(ch)) {
// 转换为小写并添加到新字符串
sgood += tolower(ch);
}
}
// 创建翻转的字符串也可以写作下面这样
string sgood_rev(sgood.rbegin(), sgood.rend());
return sgood == sgood_rev;
}
};
isalnum()函数用于检查一个字符是否是字母或数字。类似的还有isdigit()判断是否是数字;isalpha()判断是否是字母。
双指针移动比较
设置两个指针,一个指向字符串的头,一个指向字符串的尾,向中间移动,比较对应位置的字符是否相同。
需要注意的是,在移动左右指针时, 遇到非字母数字字符时,需要跳过 ,继续往下移动到下一个有效字符。
class Solution {
public:
bool isPalindrome(string s) {
int n = s.size();
int left = 0, right = n - 1;
while (left < right) {
while (left < right && !isalnum(s[left])) {
++left;
}
while (left < right && !isalnum(s[right])) {
--right;
}
if (left < right) {
if (tolower(s[left]) != tolower(s[right])) {
return false;
}
++left;
--right;
}
}
return true;
}
};
判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true
示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false
提示:
0 <= s.length <= 100
0 <= t.length <= 10^4
个字符串都只由小写字符组成。
双指针移动比较
这个子字符串的定义不同于之前的连续的子字符串,它可以不连续。思路简单直接写即可,基于长串遍历,子串也从头开始移动,遇到当前长串字符和子串的字符匹配上的,就移动一下子串的指针,比较下一个字符,子串遍历完成,即为成功,如果长串走完了还没有成功,就返回失败。
class Solution {
public:
bool isSubsequence(string s, string t) {
int n = s.size();
if (n == 0) {
return true;
}
int subPtr = 0;
for (int i = 0; i < t.size(); i++) {
// 有和子字符串相同的字符出现
if (s[subPtr] == t[i]) {
// 比较下一个
subPtr++;
// 子字符串遍历完成,结束
if (subPtr == n) {
return true;
}
}
}
return false;
}
};
两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
这题非双指针类别,但是是下一题的基础,同时也记录一下。
思路1 暴力枚举
很容易想到类似冒泡排序的写法,遍历数组,对于每个元素,都遍历数组后面的元素,看是否有和当前元素之和等于目标值的元素。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (nums[i] + nums[j] == target) {
return {i, j};
}
}
}
return {};
}
};
hash 表记录
上一个暴力解法的时间复杂度是 O(n2),主要是搜索差值的过程比较耗时。我们可以用 hash 表记录已经遍历过的元素,每次遍历到一个元素时,都去 hash 表中查找是否有和当前元素之和等于目标值的元素。如果有,就返回这两个元素的下标。时间复杂度为O(n).
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
int n = nums.size();
unordered_map<int, int> valueIndex;
for (int i = 0; i < n; i++) {
// 查看 hash 表中是否有和当前元素之和等于目标值的元素
auto it = valueIndex.find(target - nums[i]);
if (it != nullptr) {
// 找到和为目标值的元素,返回这两个元素的下标
return {it->second, i};
}
valueIndex[nums[i]] = i;
}
// 遍历完成,没有找到,返回空
return {};
}
};
两数之和II 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
提示:
2 <= numbers.length <= 3 * 104
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 1000
仅存在一个有效答案
对比第一题,要求不另外开辟空间,就只能在原数组上操作了。
同时也多了一个条件,即数组是有序的。经测试,这题如果使用暴力解法会超时。即算法时间复杂度要优于 O(n^2) .
思路1 双指针
因为数组是有序的,所以可以采用一个头一个尾,计算和值sum,与target比较,缩小范围。如果sum太小,就左指针右移,sum太大,就右指针左移。
初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和,并和目标值比较。如果两个元素之和等于目标值,则发现了唯一解。如果两个元素之和小于目标值,则将左侧指针右移一位。如果两个元素之和大于目标值,则将右侧指针左移一位。移动指针之后,重复上述操作,直到找到答案。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int n = numbers.size();
int left = 0;
int right = n - 1;
while (right > left) {
if (numbers[left] + numbers[right] > target) {
right--;
} else if (numbers[left] + numbers[right] < target) {
left++;
} else {
return {left + 1, right + 1};
}
}
return {};
}
};
复杂度分析
时间复杂度:O(n),其中 n 是数组的长度。两个指针移动的总次数最多为 n 次。
空间复杂度:O(1)。
思路2 二分查找
在数组中找到两个数,使得它们的和等于目标值,可以首先固定第一个数,然后寻找第二个数,第二个数等于目标值减去第一个数的差。利用数组的有序性质,可以通过二分查找的方法寻找第二个数。为了避免重复寻找,在寻找第二个数时,只在第一个数的右侧寻找。
low 和 high 的移动类似双指针的解法,这里是划分区间,看target落在哪里,“击中”区间后就缩小范围寻找。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
for (int i = 0; i < numbers.size(); ++i) {
int low = i + 1, high = numbers.size() - 1;
while (low <= high) {
int mid = (high - low) / 2 + low;
if (numbers[mid] == target - numbers[i]) {
return {i + 1, mid + 1};
} else if (numbers[mid] > target - numbers[i]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
}
return {-1, -1};
}
};
盛水最多的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例1:
输入:
[1,8,6,2,5,4,8,3,7]输出:49 解释:图中垂直线代表输入数组[1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
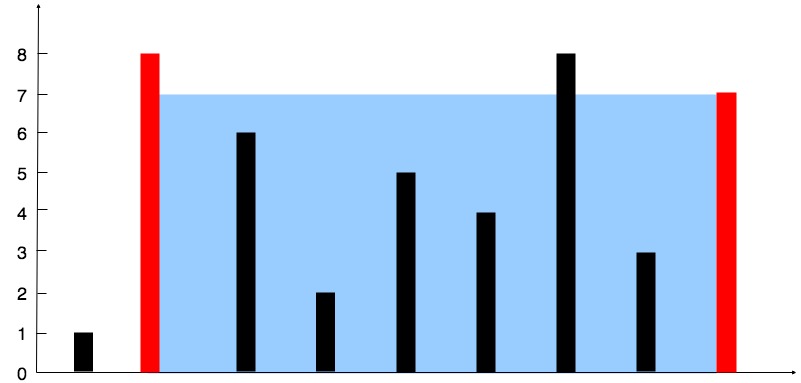
示例 2:
输入:height =
[1,1]输出:1
提示: n == height.length 2 <= n <= 105 0 <= height[i] <= 104
思路1 双指针
根据图示,可以比较容易想到使用双指针,因为做区间限制计算,需要有两个下标。
设置双指针,共同从两边开始往中间移动,直到相遇,指针移动时,记录下所组合到的最大面积 (right-left)X 短的那个指针的高度 。问题点就是该移动哪一个指针。
比较通俗的想法是,移动高度比较短的那个指针,因为移动长的那个指针,容器的高度不会增加,而宽度会减少,所以容器的面积一定是减少的。数学证明也是如此,省略证明过程。
class Solution {
public:
int maxArea(vector<int>& height) {
int n = height.size();
int left = 0;
int right = n - 1;
int maxArea = 0;
while (left < right) {
// 计算当前面积,更新maxArea的值
int areaHeight = min(height[left], height[right]);
maxArea = max(maxArea, (right - left) * areaHeight);
// 移动对应高度较短的那个指针
height[left] >= height[right] ? right-- : left++;
}
return maxArea;
}
};
复杂度分析
时间复杂度:O(N),双指针总计最多遍历整个数组一次。 空间复杂度:O(1),只需要额外的常数级别的空间。
三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
思路1 排序加双指针
题目要求找元素组合,并未对下标做限制,所以可以先排序,然后使用双指针。可以预料到时间复杂度至少为O(N^2),而sort的时间复杂度为O(NlogN),所以整体时间复杂度为O(N^2)。
求解思路类似两数之和的双指针,只是在三数之和的基础上,增加了一个循环。遍历数组时,先锁定第一个数 numbers[i] ,再设置两个指针,一个指向较小的位置(i的下一个位置),一个指向末尾,求和,如果大于0,就将right左移,如果小于0,就将left右移,知道两个指针遇上。
关于去重:
- 因为数组已经排过序,所以去重时,对第一个元素去重时,需要判断当前元素和前一个元素是否相等,如果相等,就跳过。
- 对于left这个第二位的元素,只有当匹配上一组结果了才需要去重,去重时,要看这个元素的后面一个元素是否相等,如果相等就略过,left多往右移几位,知道下一个检查的元素不相等了。
- 对于right,也是只有匹配上了才去重,看看right左边的元素与其是否相等,如果相等,就略过,right多走几步。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
int n = nums.size();
// 先排序
sort(nums.begin(), nums.end());
vector<vector<int>> result;
for (int i = 0; i < n - 2; i++) {
int lock = nums[i];
// 说明遍历到此处,后面的元素已经都大于0了
if (lock > 0) {
return result;
}
// 对第一个元素去重
if (i > 0 && lock == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = n - 1;
while (left < right) {
int sum = lock + nums[left] + nums[right];
if (sum > 0) {
// 结果大于0,缩小right指针
right--;
} else if (sum < 0) {
// 结果小于0,增大left指针
left++;
} else {
// 添加进结果数组中
result.push_back({nums[i], nums[left], nums[right]});
// 去重逻辑应该放在找到一个三元组之后,对left和right进行多移几位的操作
while (right > left && nums[right] == nums[right - 1])
right--;
while (right > left && nums[left] == nums[left + 1])
left++;
// 找到答案时,双指针同时收缩
right--;
left++;
}
}
}
return result;
}
};
移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1
进阶:你能尽量减少完成的操作次数吗?
思路1 双指针
朴素写法,遍历数组,遇到0,就将0后面的元素往前移动,然后将0放到数组的末尾。这是一个O(n^2)的算法。
使用双指针进行优化,一个指针指向当前遍历的元素,一个指针指向当前0的位置。当往前遍历的快指针遇到第一个非0元素时,就将这个非0元素移动到指向0的慢指针的位置。慢指针继续去找0,最后将尾部剩余空间全部写成0即可。
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n = nums.size();
if (n < 1) {
return;
}
int slow = 0;
for (int fast = 0; fast < n; fast++) {
if (nums[fast] == 0) {
continue;
}
nums[slow] = nums[fast];
slow++;
}
for (int i = slow; i < n; i++) {
nums[i] = 0;
}
}
};
