【AI】常见AI算法

本文介绍了若干种常见的AI领域的算法及其应用场景
前言
人工智能在GPT吹响冲锋号之后,突然迎来了关注度大爆发,在AI领域的算法也开始出现了一些新的算法,本文将介绍一些常见的AI算法及其应用场景。
首先,了解下人工智能项目的训练方法,训练方法大模型的训练需要使用深度学习方法。以下是一些常见的深度学习方法:
- 监督学习:监督学习是一种深度学习方法,其中模型被训练来预测输入数据的标签。在自然语言处理任务中,监督学习通常用于文本分类、命名实体识别、问答系统等。
- 无监督学习:无监督学习是一种深度学习方法,其中模型被训练来从数据中学习模式和特征。在自然语言处理任务中,无监督学习通常用于文本聚类、主题建模、文本生成等。
- 强化学习:强化学习是一种深度学习方法,其中模型被训练来通过与环境的交互来学习如何做出最佳决策。在自然语言处理任务中,强化学习通常用于对话系统、推荐系统等。
线性回归(Linear Regression)
线性回归是一种常见的机器学习算法,用于预测连续型变量的值。它的基本思想是通过建立一个线性模型来预测目标变量的值。
一元线性回归的过程可以表示为: \[y = \theta_0 + \theta_1x\]
多元线性回归的模型可以表示为: \[y = \theta_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n\]
其中,$y$ 是目标变量,$x_1, x_2, \cdots, x_n$ 是特征变量,$\theta_0, \theta_1, \theta_2, \cdots, \theta_n$ 是模型参数。线性回归的目标是 找到一组最优的模型参数,使得模型能够最好地拟合训练数据 。
那么,如何找到一组最优的模型参数呢?这就需要用到损失函数。损失函数是用来衡量模型预测值与真实值之间的差异的函数。常用的损失函数为均方误差(Mean Squared Error,MSE)。
均方误差的公式为: \[MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2\]
其中,$y_i$ 是第 $i$ 个样本的真实值,$\hat{y_i}$ 是第 $i$ 个样本的预测值,$n$ 是样本的数量。
图形表达:

误差从图形上看是一条线段,平方后就形成了一个正方形, 将正方形的面积求和再取平均 ,就是均方误差的损失函数。所有的正方形的平均面积越小,损失越小。对于给定数据集,x和y的值是已知的,参数m和b是需要求解的,模型求解的过程就是解公式4的过程。以上就是 最小二乘法 的数学表示,”二乘”表示取平方,”最小”表示损失函数最小。至此我们发现,有了损失函数,机器学习的过程被化解成对损失函数求最优解过程,即求一个最优化问题。
简单线性回归实践:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1, 2, 3, 4, 5], dtype=np.int8)
y = np.array([1, 3.0, 2, 3, 5])
plt.scatter(x, y)
x_mean = np.mean(x)
y_mean = np.mean(y)
num = 0.0
d = 0.0
for x_i, y_i in zip(x, y):
num += (x_i - x_mean) * (y_i - y_mean)
d += (x_i - x_mean) ** 2
a = num / d
b = y_mean - a * x_mean
y_hat = a * x + b
plt.figure(2)
plt.scatter(x, y)
plt.plot(x, y_hat, c='r')
x_predict = 4.8
y_predict = a * x_predict + b
print(y_predict)
plt.scatter(x_predict, y_predict, c='b', marker='+')
plt.show()
结果:

适用场景
什么样的数据适合使用线性回归呢?统计学家安斯库姆给出了四个数据集,被称为 安斯库姆四重奏(Anscombe’s quartet) ,分别是:

从这四个数据集的分布可以看出,并不是所有的数据集都可以用一元线性回归来建模。现实世界中的问题往往更复杂,变量几乎不可能非常理想化地符合线性模型的要求。因此使用线性回归,需要遵守下面几个假设:
- 线性回归是一个回归问题。
- 要预测的变量 y 与自变量 x 的关系是线性的(图2 是一个非线性)。
- 各项误差服从正太分布,均值为0,与 x 同方差(图4 误差不是正太分布)。
- 变量 x 的分布要有变异性。
- 多元线性回归中不同特征之间应该相互独立,避免线性相关。
回归问题与分类问题
与回归相对的是分类问题(classification),分类问题要预测的变量y输出集合是有限的,预测值只能是有限集合内的一个。当要预测的变量y输出集合是无限且连续,我们称之为回归。比如,天气预报预测明天是否下雨,是一个二分类问题;预测明天的降雨量多少,就是一个回归问题。
变量之间是线性关系
线性通常是指变量之间保持等比例的关系,从图形上来看,变量之间的形状为直线,斜率是常数。这是一个非常强的假设,数据点的分布呈现复杂的曲线,则不能使用线性回归来建模。可以看出,四重奏右上角的数据就不太适合用线性回归的方式进行建模。
误差服从正态分布
最小二乘法求解过程已经提到了误差的概念,误差可以表示为误差 = 实际值 - 预测值。 可以这样理解这个假设:线性回归允许预测值与真实值之间存在误差,随着数据量的增多,这些数据的误差平均值为0;从图形上来看,各个真实值可能在直线上方,也可能在直线下方,当数据足够多时,各个数据上上下下相互抵消。如果误差不服从均值为零的正太分布,那么很有可能是出现了一些异常值,数据的分布很可能是安斯库姆四重奏右下角的情况。 这也是一个非常强的假设,如果要使用线性回归模型,那么必须假设数据的误差均值为零的正太分布。
变量 x 的分布要有变异性
线性回归对变量 x也有要求,要有一定变化,不能像安斯库姆四重奏右下角的数据那样,绝大多数数据都分布在一条竖线上。
多元线性回归不同特征之间相互独立
如果不同特征不是相互独立,那么可能导致特征间产生共线性,进而导致模型不准确。举一个比较极端的例子,预测房价时使用多个特征:房间数量,房间数量*2,-房间数量等,特征之间是线性相关的,如果模型只有这些特征,缺少其他有效特征,虽然可以训练出一个模型,但是模型不准确,预测性差。
线性回归的优缺点
优点: (1)思想简单,实现容易。建模迅速,对于小数据量、简单的关系很有效; (2)是许多强大的非线性模型的基础。 (3)线性回归模型十分容易理解,结果具有很好的可解释性,有利于决策分析。 (4)蕴含机器学习中的很多重要思想。 (5)能解决回归问题。
缺点: (1)对于非线性数据或者数据特征间具有相关性多项式回归难以建模. (2)难以很好地表达高度复杂的数据。
逻辑回归(Logistic Regression)
逻辑回归与线性回归都是一种广义线性模型(generalized linear model,GLM)。具体的说,都是从指数分布族导出的线性模型,线性回归假设Y|X服从高斯分布,逻辑回归假设Y|X服从伯努利分布。
伯努利分布:伯努利分布又名0-1分布或者两点分布,是一个离散型概率分布。随机变量X只取0和1两个值,比如正面或反面,成功或失败,有缺陷或没有缺陷,病人康复或未康复。为方便起见,记这两个可能的结果为0和1,成功概率为p(0<=p<=1),失败概率为q=1-p。
高斯分布:高斯分布一般指正态分布。
首先我们要先介绍一下 Sigmoid函数,也称为逻辑函数(Logistic function) 。 Sigmoid函数的公式为: \[Sigmoid(x) = \frac{1}{1 + e^{-x}}\]
Sigmoid函数是一个非线性函数,它将输入值映射到0到1之间的输出值。Sigmoid函数的输出值可以被解释为概率。Sigmoid函数的图像如下:
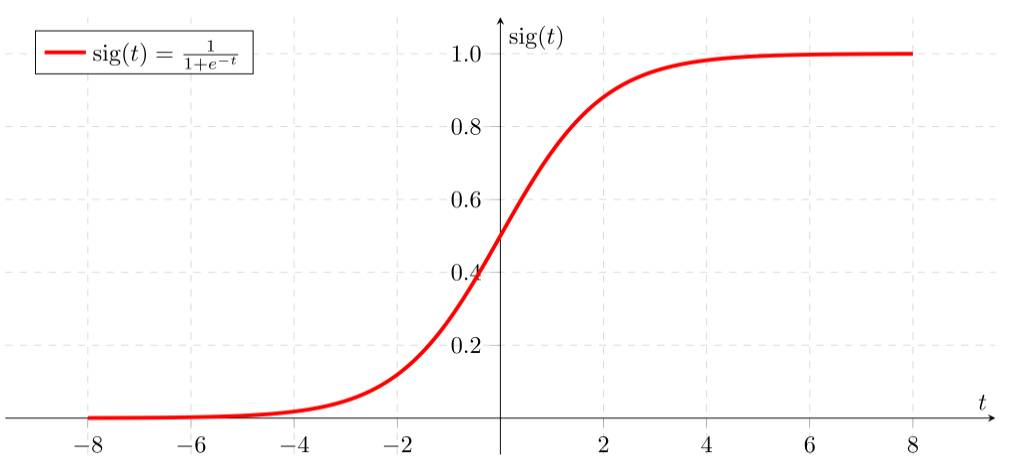
从上图可以看到sigmoid函数是一个s形的曲线,它的取值在[0, 1]之间,在远离0的地方函数的值会很快接近0或者1,它的这个特性对于解决二分类问题十分重要。
逻辑回归与线性回归有很多相同之处,去除 Sigmoid映射函数 的话,逻辑回归算法就是一个线性回归。可以说,逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
逻辑回归假设函数的形式为: \[h_\theta(x) = \frac{1}{1 + e^{-\theta^Tx}}\]
其中,$h_\theta(x)$ 是逻辑回归模型的预测值,$\theta^Tx$ 是线性回归模型的预测值。逻辑回归模型的预测值是一个概率值,它表示样本属于正类的概率。
一个机器学习的模型,实际上是把决策函数限定在某一组条件下,这组限定条件就决定了模型的假设空间。当然,我们还希望这组限定条件简单而合理。而逻辑回归模型所做的假设是: \[h_\theta(x) = P(y=1|x;\theta)\]
即在给定 x 和 θ 的条件下,y = 1的概率。
我们知道,在二分类问题模型:例如逻辑回归「Logistic Regression」、神经网络「Neural Network」等,真实样本的标签为 [0,1],分别表示负类和正类。模型的最后通常会经过一个 Sigmoid 函数,输出一个概率值,这个概率值反映了预测为正类的可能性:概率越大,可能性越大。
损失函数
通常提到损失函数,我们不得不提到代价函数(Cost Function)及目标函数(Object Function)。
- 损失函数(Loss Function) 直接作用于单个样本,用来表达样本的误差
- 代价函数(Cost Function)是整个样本集的平均误差,对所有损失函数值的平均
- 目标函数(Object Function)是我们最终要优化的函数,也就是代价函数+正则化函数(经验风险+结构风险)
概况来讲,任何能够衡量模型预测出来的值 h(θ) 与真实值 y 之间的差异的函数都可以叫做代价函数 C(θ) 如果有多个样本,则可以将所有代价函数的取值求均值,记做 J(θ) 。因此很容易就可以得出以下关于代价函数的性质:
- 选择代价函数时,最好挑选对参数 θ 可微的函数(全微分存在,偏导数一定存在)
- 对于每种算法来说,代价函数不是唯一的;
- 代价函数是参数 θ 的函数;
- 总的代价函数 J(θ) 可以用来评价模型的好坏,代价函数越小说明模型和参数越符合训练样本(x,y);
- J(θ) 是一个标量;
经过上面的描述,一个好的代价函数需要满足两个最基本的要求:能够评价模型的准确性,对参数 θ 可微。
在线性回归中,最常用的是均方误差(Mean squared error),即: \[J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2\]
而在逻辑回归中,最常用的是代价函数是交叉熵(Cross Entropy),交叉熵是一个常见的代价函数: \[J(\theta) = -\frac{1}{m}\sum_{i=1}^m[y^{(i)}log(h_\theta(x^{(i)})) + (1-y^{(i)})log(1-h_\theta(x^{(i)}))]\]
逻辑回归在确定了模型的形式后,通过最大似然估计法来实现最小散度从而求出模型参数。
为什么逻辑回归不能使用线性回归的损失函数均方差来计算呢?
线性回归的均方差损失函数是一个凸函数,可以很容易求解,而逻辑回归的损失函数是非凸函数,无法直接使用梯度下降法求解。所以逻辑回归使用的是对数损失函数(log loss function)。
LR一般需要连续特征离散化原因
- 离散特征的增加和减少都很容易,易于模型快速迭代
- 稀疏向量内积乘法速度快,计算结果方便存储,容易扩展
- 离散化的特征对异常数据有很强的鲁棒性(比如年龄为300异常值可归为年龄>30这一段)
- 逻辑回归属于广义线性模型,表达能力受限。单变量离散化为N个后,每个变量有单独的权重,相当于对模型引入了非线性,能够提升模型表达能力,加大拟合
- 离散化进行特征交叉,由 m+n 个变量为 m*n 个变量(将单个特征分成 m 个取值),进一步引入非线性,提升表达能力
- 特征离散化后,模型会更稳定(比如对用户年龄离散化,20-30作为一个区间,不会因为用户年龄,增加一岁变成完全不同的人,但区间相邻处样本会相反,所以怎样划分区间很重要)
- 特征离散化后,简化了LR模型作用,降低模型过拟合风险
逻辑回归优缺点
LR优点:
- 直接对分类的可能性建模,无需事先假设数据分布,避免了假设分布不准确带来的问题
- 不仅预测出类别,还可得到近似概率预测
- 对率函数是任意阶可导凸函数,有很好得数学性质,很多数值优化算法可直接用于求取最优解
- 容易使用和解释,计算代价低
- LR对时间和内存需求上相当高效
- 可应用于分布式数据,并且还有在线算法实现,用较小资源处理较大数据
- 对数据中小噪声鲁棒性很好,并且不会受到轻微多重共线性影响
- 因为结果是概率,可用作排序模型
LR缺点:
- 容易欠拟合,分类精度不高
- 数据特征有缺失或特征空间很大时效果不好
python例程
逻辑回归的简单例程如下:
import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
# 训练数据
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])
# 创建逻辑回归模型
model = LogisticRegression()
# 训练模型
model.fit(X, y)
# 预测新数据
new_data = np.array([[5, 6]])
prediction = model.predict(new_data)
print("预测结果:", prediction)
# 绘制训练数据
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='blue', label='Class 0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='red', label='Class 1')
# 绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.4)
# 绘制新数据的预测结果
plt.scatter(new_data[:, 0], new_data[:, 1], color='green', marker='x', label='New Data')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()
运行结果:
预测结果: [1]

